An excursion into school calculus

For reasons too boring to mention I happened to skim through the sample maths examination paper distributed by the CBSE board.

It took only a glance to see that twelfth standard maths is a greater ordeal now (progress!). Harder integrals, multiple choice questions and it seems even linear programming has entered the syllabus.

One of the questions stood out:

If $(x-a)^2 + (y-b)^2 = r^2$ , for some $r> 0$, prove that $\frac{\left(1+ \frac{dy}{dx}^2\right)^\frac32}{\frac{𝑑^2𝑦}{𝑑𝑥^2}}$ is a constant independent of $a$ and $b$.

The first expression is clearly the equation of a circle with radius $r$ centered at $(a,b)$. What explains the monstrosity with the derivatives? Is it just an examiner’s fantasy?

After some tedious algebra the student is expected to find that $M(x,y) = \frac{\left(1+ \frac{dy}{dx}^2\right)^\frac32}{\frac{𝑑^2𝑦}{𝑑𝑥^2}} = r$. Wait a minute. That’s curious, the monster makes no reference to a circle. We could plug in any curve $y(x)$, find it’s derivates and combine them in that weird expression. What would the right-hand side mean then?

That’s what we are going to find out.

Pause to think

$r$ is the radius of a circle that has the same first and second derivatives at a particular point $P$ in the curve. Imagine you’re driving a car along that curve steering carefully to stay on it. When you hit P, keep the steering wheel locked in place. Your car will continue to travel in the osculating circle. The name comes from the Latin osculare: to kiss, and certainly ranks in my top-ten mathematical terms.

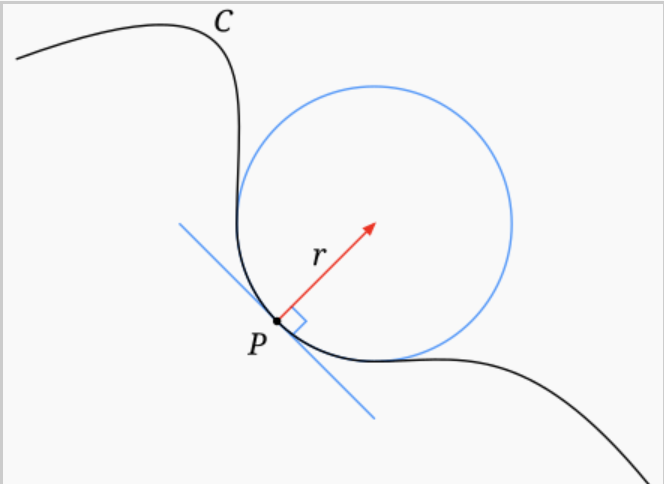
osculating circle

But where does the monster come in? From the car analogy we suspect that a turning angle is involved. We know that the $\text{slope} = \frac{dy}{dx} = \tan\theta$, measuring $\theta$ with respect to the x axis. How fast is it changing?

\[\begin{align*} \theta &= \arctan{\frac{dy}{dx}} \\ \frac{d\theta}{dx} &= \frac{\frac{d^2y}{dx^2}}{\left[1+\left(\frac{dy}{dx}\right)^2\right]} \qquad \text{using our beloved chain rule} \end{align*}\]

That’s close but a closer look reveals that we are missing a factor of $\left[1+\left(\frac{dy}{dx}\right)^2\right]^{1/2}$ compared to the expression in the monster. The reason is that we haven’t thought carefully about what to measure $\theta$ against. The $x$ coordinate is not special - the car doesn’t “know” about it.

Pause - what does the car know?

A far more natural option is the arc-length - the continuous distance travelled along the curve. It’s right there on the odometer (Greek: hodos:road). In a little time-step the car moves by $\delta x$ and $\delta y$ in the x and y directions. We start with Pythagoras to get the arc-distance $\delta s$.

\[\begin{align*} \delta s^2 &=& \delta x^2 + \delta y^2 \\ &=& \delta x^2 \left(1 + \frac{\delta y^2}{\delta x^2}\right) \\ \frac{\delta s^2}{\delta x^2} &=& 1 + \frac{\delta y^2}{\delta x^2} \\ \left(\frac{ds}{dx}\right)^2 &=& 1 + \left(\frac{d y}{d x}\right)^2 \\ \frac{ds}{dx} &=& \sqrt{1 + \left(\frac{d y}{d x}\right)^2} \end{align*}\]

where we took limits to zero and turned $\delta$’s to $d$ ‘s.

Finally we can compute $\frac{d\theta}{d s}$ - how fast we are turning with respect to the arc-length.

\[\frac{d \theta}{d s} = \frac{d \theta}{dx}\frac{dx}{ds} = \frac{d\theta}{dx}/\frac{ds}{dx} = \frac{\frac{d^2y}{dx^2}}{\left[1+\left(\frac{dy}{dx}\right)^2\right]^\frac32}\]

Viola, here is the monster or rather, 1 over it. Amazingly it has quite a natural interpretation and goes by the name of curvature. This formula was derived by Newton around 1671.

More questions